I just moved into an off-campus apartment in Atlanta. I bought a bed from Ikea, the closet came with a shelving unit, but I didn't see any desks I particularly liked or could afford. My parents had one or two desks with tops I could have resized, but I wasn't particularly fond of the surface finishes, and I thought it'd be fun to get my hands dusty and build my own on the cheap. I had seen lots of people around the internet doing stuff with pallets, so I decided to see what all the rage was.

My girlfriend and I searched around campus a few weeks ago in various dumpsters and managed to fill up the back of my Dad's car with 10 clean, dry pallets. The next weekend we got them home and started processing the pallets into useable wood. We tried a few times to use a crowbar to get the cross members off and remove the nails, but most of the boards were cracking unless we pried up each nail slowly. We took an alternative approach and cut the planks out on either side of the braces.

I wanted to take a different, more aesthetically pleasing approach to pallet projects. Instead of using the bare pallets as supports, and using the entire width of the wood as the surface, I wanted to create more of a butcher-block look. To this, I needed to process the wood down into thin strips of equal height and equal thickness.

A generous neighbor lent me his planer. I ripped everything down to just shy of 3/8". I was changing the height of the planer so frequently, I wanted to do a last pass at exactly 3/8" on every plank without changing the height. As a side note, planers are awesome. It took super gross wood and turned it into wood I could have bought from a lumber supply company. It was kind of cathartic actually. Look at all the beautiful wood!

Next, I needed to rip each piece into 1 1/4" wide strips. I could have used the table saw to rip an edge on each of them, but it would have taken lots of adjusting of the saw. Instead, my father showed me a trick on the router table. We used some washers to offset the output-side of the router forward from the feed-side. The output-side guide was aligned with the outside of the straight router bit, while the feed-side guide was slightly behind it. When a piece of wood is passed through the router table, a slight amount of material is taken off the side of the piece, and the new edge rests up against the output-side fence. This prevents the piece from teetering on the bit. It's basically a router table set up as a joiner. After a pass or two through the router an edge that looked like this:

Looks like this:

With this perfect edge, it was easy to keep the table saw set up at 1 1/4" to rip each plank into strips. All that was left was to square the edges off with a miter saw. Here's what the wood looked like at this point. (Shout out to Dad and Valerie for their crazy amount of help.)

We then spent a little while figuring out how we wanted the desk to look. I had some darker pieces (which I think are Ash, not sure), so I put those at a somewhat even number of rows away from another to add some nice accents to the desk.

We returned the next weekend to glue. This process was slow and stressful. I think we clamped the planks too hard, and didn't take enough precautions to make sure that the clamps covered the entire height of the desk. We didn't notice until around the end that the pieces had started slanting in one direction. We couldn't come up with a way of fixing this, so the last few strips we glued we glued onto the row we started with, which was still 90° to the gluing surface. It should end up fine (hopefully). The most important things we found were that

1. The glue cures faster than you think, and once you've done three or four rows, you can't really move the strips in the middle. So before you continue gluing the next row, push on the end of the row to make sure that all of the sides are butted up against one another.
2. Make sure the strips are pushed down towards the surface you're gluing on.
3. Don't clamp too hard, and make sure the clamp is clamping the centers together, not compressing the bottom or top of the strips more.
4. Buy a lot of glue. The table is held together with about three bottles of wood glue.

Now here's the fun part. Sanding. We used a scraper to get most of the big chunks of glue off. We should have bene more diligent about wiping the glue off with a damp towel, this would have reduced the number of big glue chunks on the surface. Also helpful was a rasp to get lots of material off quickly. The top of the table was anything but flat. Lots of pieces were not completely pushed down onto the surface I was gluing on, and due to the slanting problem we had the last few rows were significantly lower than the others. Belt sanders, loud music and patience are helpful tools.

There's still a lot of sanding to do. I need to keep using the rougher grit sandpaper to level the surface off as best as I can. I'm continuously dragging a level across the surface to check for dips, though it's a time consuming process. After the surface is mostly flat, I'll be taking 120 grit to it using the belt sander, in long even strokes, and then after that a random orbital with 240 grit and possibly a few passes higher. I didn't get enough pallets to get quite the depth that I wanted, so I'll be adding a trim of ripped 2x4s or something around the edges. Hopefully the edges will give it some strength, because I am slightly worried about the glue holding the table together against weights placed in the middle. For legs, I'll probably be ordering some hairpin legs off the internet, though this hasn't been decided yet.

For the surface finish, I'll either go with simply tung oil and call it a day (easiest, but the surface isn't very hard, so pen strokes will transfer), or give it a coat of varnish or polyurethane. Also haven't decided this yet. Either way, I'm super happy with how it's turning out so far.

I've wanted to write a compiler for a while now. I'm fascinated with how code can be processed into something that is understood natively by a processor. I'm less fascinated with interpreters, which is unfortunate, since there seems to be a lot more material on writing an interpreter and interpreter design on the internet. It makes sense. They're easier to write. Code can be processed incrementally, and really, it's just a translation of one language's actions into another.

Compilers on the other hand, generate completely stand-alone code. In a sense, you're still writing an interpreter, as the compiler is tasked simply with a translation job. The complexity comes from the translation being between a relatively high level to the lowest possible level (somewhat).

Before actually trying to implement a compiler, I need to do some reading. I did some preliminary reading, and I've decided that I'll have the greatest chance of success if I choose a language with a relatively simple grammar. C is pretty simple, especially if you omit some of the fancier stuff (flexible declaration locations, function pointers, inline functions) but it's still pretty long. I chose Scheme. The grammar consists basically of two parenthesis, number, character, and boolean literals, and identifiers. Everything else is a function (within some obvious limits, looking at you, macros).

You can write a compiler for scheme and then implement the core functions as you go. In fact, the scheme interpreter I'm using to learn scheme, gambit (which is also a compiler), omits lots of common functions found in the MIT scheme interpreter. If you look at the string library for MIT Scheme, you can count on about 80% of the functions on the page not being available in gambit.

Onto the fun part.

I decided to start tackling Project Euler problems to learn Scheme. I've always found that the first 10-20 problems pretty much put you through a language's paces. You can see my current progress on github in my projectEuler repository (no cheating!). Not only have I learnt a lot of Scheme over the last few weeks, I've learned a lot about functional programming, and it's been a real mental challenge to warp my mind into the functional way of thinking.

I thought I'd showcase a few of the cool things that I did, and some of the novel (probably convoluted approaches) I took.

starting simple : problem #1

;;Project Euler Problem #1
;; If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5,
;; 		6 and 9. The sum of these multiples is 23.
;; Find the sum of all the multiples of 3 or 5 below 1000.
;;
;; Answer : 233168

;;v2
(begin
    (define sumDivisibleBy (lambda (n end)
        (let ((count (quotient end n)))
            (* count (+ count 1) 0.5 n))))
    (display (- (+ (sumDivisibleBy 3 999) (sumDivisibleBy 5 999)) (sumDivisibleBy 15 999)))
    (newline)
)

So, this one's pretty simple. We define a function that finds the sum of all numbers divisible by n that are less than end. We know that n can fit into end end/n times (fourth grade here), so we simply use the formula for the sum of a series of integers to find the sum of the numbers, then multiply that by n. Simple enough.

interesting discoveries: problem 3

Problem 3 isn't really important to this following bit of code. I was planning on writing a prime sieve for this problem, for memoization of the prime factorization algorithm (to keep it from continuously rechecking if a number was prime), but sieves are usually useful when you know the upper bound that you need to target. You could stop and re-sieve with a higher bound, but I didn't want to muck around with that logic at the time.

Anyway, here's an interesting range function:

; returns a list containing every 'increment' integer between
;	start (inclusive) and end (exclusive)
(define range (lambda (start end increment)
    (if (not (or (and (< start end) (> increment 0)) (and (> start end) (< increment 0))))
        '()
        (begin
            (if ((if (< start end) > <=) start end)
                '()
                (begin
                    (cons start (range (+ start increment) end increment))))))))

Again, MIT-scheme provides a method quite like this built-in, but gambit did not. I think the lack of a huge library really helped me learn better. I was continuously forced to go and write methods that would have otherwise been provided for me.

The interesting thing here is in the second if statement, and in the recursiveness (it's a really slow range function, I wrote a faster one using vectors later) of the function. The first conditional checks to make sure that the function wasn't called with an increment = 0 or a lower bound that is greater than the upper bound for increment > 0 and vice versa. It returns an empty list ('()) if these checks fail. The second if statement checks to make sure that the function is still within the bounds of the range. That is, if start < end for increment > 0 or vice versa. What's interesting about it, is that there is an if inside an if which returns an operator for the outer if to use.

(if (< start end) > <=)

This code will cause the outer if statement to compare the start and end with the appropriate comparator.

However, it should be noted that this code could also be written much more concisely as:

(if (= start end))

But isn't the code above so much cooler?

fun with map and apply: problem 6

This problem is simple, for the first 100 natural numbers, find the difference between the sum of squares and the square of the sum. Hey, didn't I just write a range function? This one was super simple.

(define findDiff (lambda (n)
    (let* (
        (sumSquares (apply + (map (lambda (n) (expt n 2)) (range 1 (+ n 1) 1))))
        (squareSum (expt (apply + (range 1 (+ n 1) 1)) 2)))
        (- squareSum sumSquares))))

The sum of squares is simply mapping a lambda that is, sort of currying expt with a power of 2 over the range, and then applying the + function to the resulting list. The square of the sum is even easier, we just apply + to a range, and then call expt. Take the difference, and that's the sum of the squares.

hard mode: problem 5

This problem was strangely harder than problem 6, but it's probably more in the way I solved it. The challenge is to find the first number that's divisible by all numbers 1 through 20. I'm not going to show all the code here. I'll explain the helper functions used, but there's too much code to put in one place. In actuality, the solution boils down to five lines that process lists.

The math involved is pretty hairy, so I'll summarize it. Turns out, to find the LCM of two numbers, you can use their prime factorizations. For each prime number that is represented in the factorizations, find the highest power it is raised to, then multiply each prime that is represented raised to it's highest power.

(define findFirstDivisibleUpTo (lambda (u)
    (let* (
        (factorizations (map (lambda (n) (hist-supplement '() n)) (map factorize (range 2 (+ u 1) 1))))
        (neededPrimes (filter prime? (range 2 (+ u 1) 1)))
        (counts (map (lambda (p) (map (lambda (n) (hist-get-value n p)) factorizations)) neededPrimes))
        (greatestCounts (map greatest counts)))
        (apply * (map (lambda (n) (expt (list-ref neededPrimes n) (list-ref greatestCounts n))) (range 0 (length neededPrimes) 1))))))

(display (findFirstDivisibleUpTo 20))(newline)

This is probably terrible code, but I just absolutely love the process that used here. It follows the mathematical process almost exactly.

The first line does a lot,

(factorizations (map (lambda (n) (hist-supplement '() n)) (map factorize (range 2 (+ u 1) 1))))

On the far right, we map the factorize function onto a range from 2 to u (the argument to the findFirstDivisibleUpTo function). factorize returns a list containing the prime factorization of a number. This generates a list of lists. Then, for each list (which contains a prime factorization) we map the hist-supplement function onto it. This function accepts a histogram, and supplements a list of numbers into it, the number of times the number appears in the argument is the frequency of that number which is supplemented into the histogram. A histogram is a list with dotted pairs that contain the frequency that each number appears. So, what this code has done has generated found the power that each prime is raised to in each prime factorization.

Here's some sample execution.

↪ gsi
Gambit v4.7.3

> (load "5.scm")
> (factorize 40)
(2 2 2 5)
> (hist-supplement '() '(5 5 2))
((2 . 5) (1 . 2))
> (map factorize (range 2 21 1))
((2)
 (3)
 (2 2)
 (5)
 (2 3)
 (7)
 (2 2 2)
 (3 3)
 (2 5)
 (11)
 (2 2 3)
 (13)
 (2 7)
 (3 5)
 (2 2 2 2)
 (17)
 (2 3 3)
 (19)
 (2 2 5))
> (map (lambda (n) (hist-supplement '() n)) (map factorize (range 2 21 1)))
(((1 . 2))
 ((1 . 3))
 ((2 . 2))
 ((1 . 5))
 ((1 . 2) (1 . 3))
 ((1 . 7))
 ((3 . 2))
 ((2 . 3))
 ((1 . 2) (1 . 5))
 ((1 . 11))
 ((2 . 2) (1 . 3))
 ((1 . 13))
 ((1 . 2) (1 . 7))
 ((1 . 3) (1 . 5))
 ((4 . 2))
 ((1 . 17))
 ((1 . 2) (2 . 3))
 ((1 . 19))
 ((2 . 2) (1 . 5)))

Now, just for bookkeeping, we need a list of possible primes we could have encountered while calculating the prime factorizations of the first u numbers. This one is simple, it requires a filter function which I wrote, it's a classic filter, it returns a new list containing only elements in the source list for which a function returned true for.

(neededPrimes (filter prime? (range 2 (+ u 1) 1)))

Here's what we get if we run this line.

> (filter prime? (range 2 21 1))                    
(2 3 5 7 11 13 17 19)

Here's where it gets fun. The next line kind of rotates the factorizations list into a matrix. A nested mapping is performed. For every prime number in needed primes, we map the hist-get-value function onto the factorizations list. This means for each prime number, we get a list of exponents that that prime is raised to in each factorization, 2 through u. This is handy, and you'll see why in the next step.

> (map (lambda (p) (map (lambda (n) (hist-get-value n p)) factorizations)) neededPrimes)
((1 0 2 0 1 0 3 0 1 0 2 0 1 0 4 0 1 0 2)
 (0 1 0 0 1 0 0 2 0 0 1 0 0 1 0 0 2 0 0)
 (0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1)
 (0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0)
 (0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0)
 (0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0)
 (0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0)
 (0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0))

Remembering the algorithm, we needed to figure out the highest power that each prime was raised to. This is, thankfully, a simple mapping. I wrote a greatest function that returns the greatest number in list, and I map it over each list above.

> (map greatest counts)                  
(4 2 1 1 1 1 1 1)

Now we're getting somewhere. We have that list of primes that were represented, so, now it's just a matter of raising each prime in that list to the corresponding power, and then multiplying them together.

> (apply * (map (lambda (n) (expt (list-ref neededPrimes n) (list-ref greatestCounts n))) (range 0 (length neededPrimes) 1))))))
232792560

This method is hilariously fast. And Scheme's native handling of large numbers is awesome (especially for Project Euler).

↪ time gsi upTo1000Test.scm
7128865274665093053166384155714272920668358861885893040452001991154324087581111499476444151913871586911717817019575256512980264067621009251465871004305131072686268143200196609974862745937188343705015434452523739745298963145674982128236956232823794011068809262317708861979540791247754558049326475737829923352751796735248042463638051137034331214781746850878453485678021888075373249921995672056932029099390891687487672697950931603520000
        0.54 real         0.51 user         0.01 sys

Compared to the brute force approach, it's nowhere close. For perspective, the brute force solution takes ~25 seconds to find the first number that is divisible 1-20. Though to be honest I wasn't going for speed here. I just found it interesting. What's neat is that, as soon as I read the description of the algorithm on Wikipedia, my mind instantly started thinking in terms of lists and mappings. My brain has become infected with Scheme.

where now?

I think I'm pretty comfortable with Scheme now. In fact, I probably could have stopped a while ago. The next step is reading the Dragon Book so I can start writing a compiler. I've found a copy and have started taking notes while I'm on trains and when I have idle moments. I've put the notes I'm taking up on github in the sssc repository under the lit section. Ideally I'll put the notes up for each chapter that I read, along with homework problems and solutions.

goals

I initially want to just get a lexer and a parser working. Then I'll begin working on the intermediate representation. After that, I'll focus on code generation for MIPS, since I have an emulator I'm comfortable with from a class I took (ECE 2035, in the readme there's a guide to setting up an executable copy of MiSaSiM).

After MIPS... well, I think it'd be fun to generate AVR assembly, or possibly PIC assembly (for the MPLAB assembler). That way I could actually write some code for an ATMega or PIC16 in Scheme, which would be quite fun actually.

Way further down the road, probably after I've taken my advanced computer architecture class, and another VLSI class, I'd like to actually come up with my own simple architecture and simple assembler, with an implementation in Verilog, and then target that. That way I could have built pretty much an entire system. So, we'll see where this goes. I'm excited for now.

Spotify has this really great collaborative playlist feature. I have a few of them with various friends and it's allowed me to find a lot of great new music. I have one with two friends, and because I'm literally in love with Spotify (maybe it's because I can't come up with any other good ideas at the moment). Since I just learned how to work with the EchoNest libraries, I figured I'd do something with that.

I wanted to use Node, and the wrapper libraries for libSpotify that I could find were good, but none of them had ported the whole library, specifically, I wanted to know the users that had added the songs to the playlist, and the times they were added. I suppose I could have contributed to their codebase, but I wanted to get something done quick and dirty, so I used used libSpotify with C, and wrote a CLI program that output information in a ~SV (tilde separated) format which could be parsed by Node. A little hacky, but it got the job done.

//need to link in the libspotify library when compiling
//cc datagrabber.c -I/usr/local/opt/libspotify/include -L/usr/local/opt/libspotify/lib -lspotify -o datagrabber

#import <libspotify/api.h>
#import <stdio.h>
#import <stdlib.h>
#import <unistd.h>
#import <ctype.h>


const uint8_t g_appkey[] = {}; // get your own appkey!

const size_t g_appkey_size = sizeof(g_appkey);
int g_logged_in;
int g_playlist_loaded;
int g_userinfo_loaded;


static void logged_in(sp_session *session, sp_error error)
{
    g_logged_in = 1;
}

static void connection_error(sp_session *session, sp_error error)
{
    fprintf(stderr, "connection error");
}

static void playlist_state_changed(sp_playlist *playlist, void *userdata) {
    if(sp_playlist_is_loaded(playlist)) {
        g_playlist_loaded = 1;
    }
}

int main() {
    char playlistURI[100];
    fscanf(stdin, "%s", playlistURI);

    sp_session_callbacks callbacks = (sp_session_callbacks) {
        .logged_in = &logged_in,
        .logged_out = NULL,
        .metadata_updated = NULL,
        .connection_error = &connection_error,
        .message_to_user = NULL,
        .notify_main_thread = NULL,
        .music_delivery = NULL,
        .play_token_lost = NULL,
        .log_message = NULL,
        .end_of_track = NULL,
        .streaming_error = NULL,
        .userinfo_updated = NULL
    };

    sp_session_config config = (sp_session_config){
        .api_version = SPOTIFY_API_VERSION,
        .cache_location = "",
        .settings_location = "",
        .application_key = g_appkey,
        .application_key_size = g_appkey_size,
        .user_agent = "playlist finder",
        .callbacks = &callbacks,
        .userdata = NULL
    };

    sp_session *session;
    sp_error error = sp_session_create(&config, &session);

    if(error != SP_ERROR_OK) {
        fprintf(stderr, "Error: Cannot create session.\n");
    }
    

    g_logged_in = 0;
    sp_session_login(session, "mattegan", "***", 0, NULL);
    
    int next_timeout = 0;	
    while(!g_logged_in) {
        sp_session_process_events(session, &next_timeout);
    }

    g_playlist_loaded = 0;

    sp_link *playlistLink = sp_link_create_from_string(playlistURI);
    sp_playlist *playlist = sp_playlist_create(session, playlistLink);


    sp_playlist_callbacks playlistCallbacks = (sp_playlist_callbacks){
        .playlist_state_changed = &playlist_state_changed
    };

    sp_playlist_add_callbacks(playlist, &playlistCallbacks, NULL);

    while(!g_playlist_loaded) {
        sp_session_process_events(session, &next_timeout);
    }

    int num_tracks = sp_playlist_num_tracks(playlist);
    for(int i = 0; i < num_tracks; i++) {
        sp_track *track = sp_playlist_track(playlist, i);
        while(!sp_track_is_loaded(track)) {
            sp_session_process_events(session, &next_timeout);
        };

        sp_link *trackLink = sp_link_create_from_track(track, 0);
        char linkString[200];
        sp_link_as_string(trackLink, linkString, 200);
        
        sp_user *user = sp_playlist_track_creator(playlist, i);

        while(!sp_user_is_loaded(user) || !isalpha(sp_user_display_name(user)[0])) {
            sp_session_process_events(session, &next_timeout);
        }

        sp_album *album = sp_track_album(track);

        while(!sp_album_is_loaded(album)) {
            sp_session_process_events(session, &next_timeout);
        }

        sp_artist *artist = sp_album_artist(album);

        while(!sp_artist_is_loaded(artist)) {
            sp_session_process_events(session, &next_timeout);
        }
        
        //line output format
        //	spotifyURI~user_canonical_name~user_display_name~track_name~artist_name~album_name~track_duration~track_add_time

        printf("%s~", linkString);
        printf("%s~%s~", sp_user_canonical_name(user), sp_user_display_name(user));
        printf("%s~%s~%s~", sp_track_name(track), sp_artist_name(artist), sp_album_name(album));
        printf("%i~", sp_track_duration(track));
        printf("%i\n", sp_playlist_track_create_time(playlist, i));

    }

    return 0;
}

This looks super complicated, but in reality it's not. Most of it is just dealing with the specifics of libSpotify, which is fairly straightforward. The only confusing bit may be the following:

while(!g_logged_in) {
    sp_session_process_events(session, &next_timeout);
}

This is libSpotify's strange event handler. It's blocking. CocoaLibSpotify abstracts all of this event handling out to GCD threads, which is pretty nice. Here it doesn't really matter, the node code just waits however long it's going to take, there's not much it can do in the meantime really. The output of this program is a few hundred lines of:

spotify:track:7AvbfnZNXylSfjDgFG5vyW~mattegan~mattegan~Wooden Heart~Listener~Wooden Heart~248000~1389368504
spotify:track:7dbgHt3XQgALzwA1BqGMdi~mattegan~mattegan~Honeybee~Seahaven~Winter Forever~250000~1389368504

Each line contains a Spotify URI, which can be used to locate the song using the foreign library IDs on the EchoNest, the username and the display name for the user who added the song, the track's artist, title and album name, the duration of the song, and the time that it was added to the playlist. For each of these lines, the JS code requests information about each song from the Echonest. Instead of making hundreds of requests, it adds the songs into a taste profile, because the EchoNest has an endpoint for getting track information for all of the songs in a profile. I construct a taste profile for each user that contributing to the playlist, this way I can do some more interesting things in terms of providing each user recommendations, which I haven't actually used yet. Mainly, it allowed for me to place the information I got from libSpotify into the foreign key item for each track in the taste profile, which meant that once I got information back from the EchoNest, I didn't have to re-correlate it to the data I got from Spotify. Kind of cheating I suppose.

You have to wait a while for the EchoNest to processes each song in the taste profile. So the JS code makes requests every half second or so to an endpoint that allows for checking the processing status of a profile, I do this for each profile I've assembled, using a status code that the EchoNest gives every time you add information into it.

//this function checks the status of a taste profile and calls the callback when the update progress is 100%
function waitForTasteProfileUpdate(tasteProfileUpdateTicket, callback) {
  var check = function() {
    var checkTasteProfileStatusRequest = {
      url:  'http://developer.echonest.com/api/v4/tasteprofile/status',
      qs:   {
        api_key: echonestApiKey,
        ticket: tasteProfileUpdateTicket
      }
    }
    request(checkTasteProfileStatusRequest, function(error, response, body) {
      var response = JSON.parse(body).response;
      if(response.ticket_status === 'complete') {
        callback();
      } else{
        console.log(tasteProfileUpdateTicket + 'percent complete: ' + response.percent_complete);
        setTimeout(check, 500);
      }
    })
  }
  check();
}

Okay, so, to the point really. After I had all this data back I made some pretty graphs. That's about it. Here's one showing the times that people had been adding songs into the playlist. As you can see, I need to get to bed earlier.

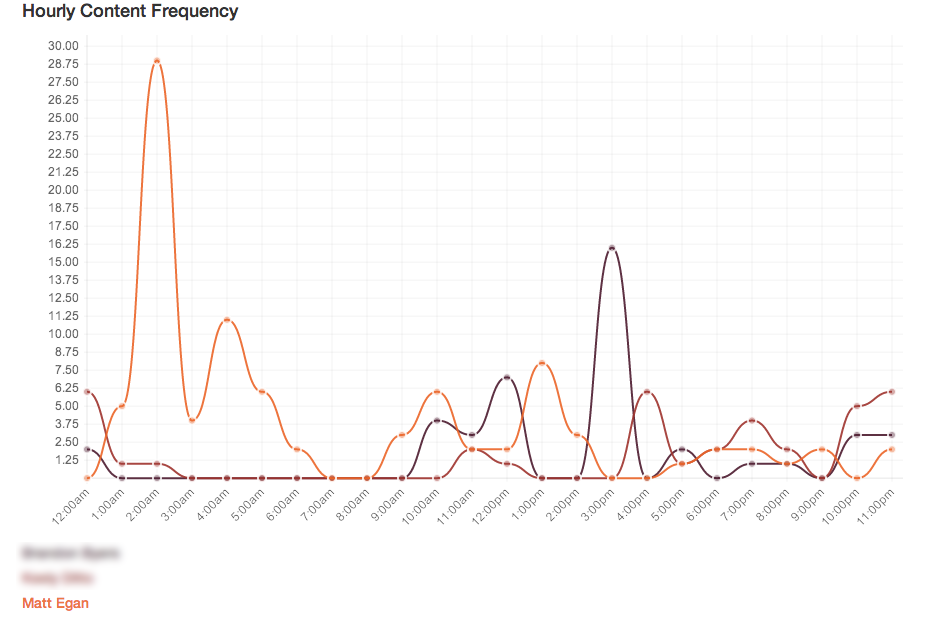
Here's a tempo distribution for the collaborative playlist.

Turns out, a lot of the plots are not very interesting. The EchoNest also keeps track of a "hotttness" rating for a track and it's artist, and lots of us listen to artists that aren't very hot. We're dirty hipsters. Here's one that's particularly telling though (though, I have to admit, a total misapplication of the plot type).

I told you we were all dirty hipsters.